一、重积分的几何意义是什么
二重积分的几何意义是曲顶柱体的有向体积,物理意义是加在平面面积上压力(压强可变);三重积分的几何意义和物理意义都认为是不均匀的空间物体的质量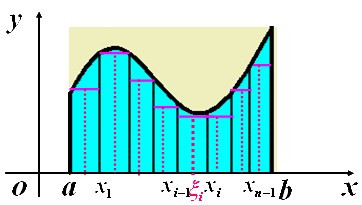
多重积分是定积分的一类,它将定积分扩展到多元函数(多变量的函数)。多重积分具有很多与单变量函数的积分一样的性质(线性,可加性,单调性等等)。多重积分问题的解决在多数情况下依赖于将多重积分转化为一系列单变量积分,而其中每个单变量积分都是直接可解的。
二、用定积分的几何意义求解 求详细过程谢谢了
一、几何意义:本定积分属于一重定积分,其几何意义为在求闭区间内函数曲线与x轴围成图形的面积。
二、本题分析:因为被积函数为非负数,积分区间为[0,1],所以定积分为位于第一象限内的以坐标原点为圆心,半径为1的1/4圆的面积。
三、圆的面积:pi*r*r,r=1,所以圆的面积为pi。
四、积分结果:pi/4。
三、积分的几何意义是什么?
(1)若f(x)≥0,x∈[a,b],∫(a→b)f(x)dx的几何意义是曲线y=f(x),x=a,x=b,y=0围成的曲边梯形的面积;
(2)若f(x)≤0,x∈[a,b],∫(a→b)f(x)dx的几何意义是曲线y=f(x),x=a,x=b,y=0围成的曲边梯形的面积的相反数;
(3)若f(x)在区间[a,b]上有正有负时,∫(a→b)f(x)dx的几何意义为曲线y=f(x)在x轴上方部分之下的曲边梯形的面积取正号,曲线y=f(x)在x轴下方部分之上的曲边梯形的面积取负号,构成的代数和。
积分是微积分学与数学分析里的一个核心概念。通常分为定积分和不定积分两种。直观地说,对于一个给定的正实值函数,在一个实数区间上的定积分可以理解为在坐标平面上,由曲线、直线以及轴围成的曲边梯形的面积值(一种确定的实数值)。
积分的一个严格的数学定义由波恩哈德·黎曼给出(参见条目“黎曼积分”)。黎曼的定义运用了极限的概念,把曲边梯形设想为一系列矩形组合的极限。从十九世纪起,更高级的积分定义逐渐出现,有了对各种积分域上的各种类型的函数的积分。
比如说,路径积分是多元函数的积分,积分的区间不再是一条线段(区间[a,b]),而是一条平面上或空间中的曲线段;在面积积分中,曲线被三维空间中的一个曲面代替。对微分形式的积分是微分几何中的基本概念。
四、积分,二重积分,三重积分,它们的几何意义与物理意义各是什么
定积分的几何意义是曲边梯形的有向面积,物理意义是变速直线运动的路程或变力所做的功。
二重积分的几何意义是曲顶柱体的有向体积,物理意义是加在平面面积上压力(压强可变)。
三重积分的几何意义和物理意义都认为是不均匀的空间物体的质量。
积分的线性性质:
性质1 (积分可加性) 函数和(差)的二重积分等于各函数二重积分的和(差),即
性质2 (积分满足数乘) 被积函数的常系数因子可以提到积分号外,即 (k为常数)
比较性:
性质3 如果在区域D上有f(x,y)≦g(x,y),则
估值性:
性质4 设M和m分别是函数f(x,y)在有界闭区域D上的最大值和最小值,σ为区域D的面积,则
性质5 如果在有界闭区域D上f(x,y)=k(k为常数),σ为D的面积,则Sσ=k∫∫dσ=kσ。
二重积分中值定理:
设函数f(x,y)在有界闭区域D上连续,σ为区域的面积,则在D上至少存在一点(ξ,η),使得
扩展资料:
二重积分和定积分一样不是函数,而是一个数值。因此若一个连续函数f(x,y)内含有二重积分,对它进行二次积分,这个二重积分的具体数值便可以求解出来。
如函数 ,其积分区域D是由 所围成的区域。
其中二重积分是一个常数,不妨设它为A。对等式两端对D这个积分区域作二重定积分。
故这个函数的具体表达式为:f(x,y)=xy+1/8,等式的右边就是二重积分数值为A,而等式最左边根据性质5,可化为常数A乘上积分区域的面积1/3,将含有二重积分的等式可化为未知数A来求解。
设Ω为空间有界闭区域,f(x,y,z)在Ω上连续。
(1)如果Ω关于xOy(或xOz或yOz)对称,且f(x,y,z)关于z(或y或x)为奇函数,则:
(2)如果Ω关于xOy(或xOz或yOz)对称,Ω1为Ω在相应的坐标面某一侧部分,且f(x,y,z)关于z(或y或x)为偶函数,则:
(3)如果Ω与Ω’关于平面y=x对称,则:
参考资料:百度百科——三重积分
参考资料:百度百科——二重积分







