一、余角的定义和性质是什么？
余角的定义和性质是：余角是如果两个角的和等于90°（直角），就说这两个角互为余角，即其中每一个角是另一个角的余角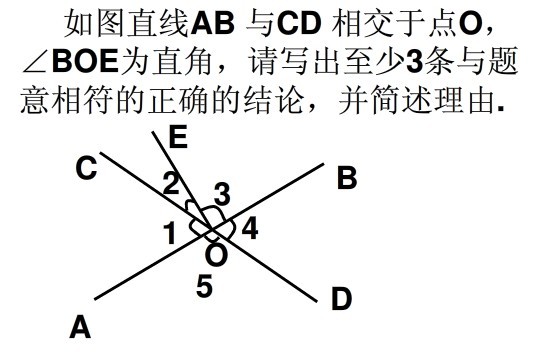
余角的性质：同角（或等角）的余角相等。
余角是不能单独出现的，只能说角A和角B互为余角或者角A是角B的余角，但不能说角A为余角。
余角和补角的性质：
两个角和为90度这两个角互为余角，两个角的和为180度，这两个角互为补角，可看出余角和补角说的都是两角关系，所似余角和补角的定义就号它们的性质
余角性质：同角的余角相等，比如：∠A+∠B=90°，∠A+∠C=90°，那么∠C=∠B。等角的余角相等，比如：∠A+∠B=90°，∠D+∠C=90°，∠A=∠D，那么∠C=∠B。
补角性质：同角的补角相等，比如：∠A+∠B=180°，∠A+∠C=180°，那么∠C=∠B。等角的补角相等，比如：∠A+∠B=180°，∠D+∠C=180°，∠A=∠D，那么∠C=∠B。
二、余角的定义?
如果两个角的和是直角（90°）,那么称这两个角“互为余角”,简称“互余”,也可以说其中一个角是另一个角的余角.两角度数之和为90°,就说明这两个角互为余角.
三、余角是什么意思？
余角释义：两角之和等于直角（90˚）时，这两个角互为余角。如直角三角形的两锐角互为余角。
若∠A +∠C=90°，即有：
∠A=90°－∠C，∠C=90°－∠A，
从而∠A的余角=90°－∠A，∠C的余角=90°－∠C。
备注：数学中互余的两个角都是锐角，不能是直角、钝角或平角等。余角是不能单独出现的，只能说角A和角B互为余角或者角A是角B的余角，但不能说角A为余角。
扩展资料：
1、同角或等角的余角相等。
若∠A+∠B=90°，∠D+∠C=90°，∠A=∠D
则有∠C=∠B。即得等角的余角相等。
2、关于余角的三角函数结论：
若 ∠A+∠B=90°，则有sinA=cosB，cosA=sinB；tanA×tanB=1。
若有一角∠α，使得∠β与∠α有如下关系：∠β+∠α=90°
且有一∠γ，使得∠β与其有如下关系：∠β+∠γ=180°
则我们可以说∠γ是∠α的余角的补角。
如果两个角的和是直角，那么称这两个角互为余角；如果两个角的和是平角，那么称这两个角互为补角。
同角（等角）的余角（补角）相等。
参考资料来源：百度百科——余角
四、什么是余角什么是
解：
余角，数学名词。如果两个角的和是直角（90°+180°k,k∈Z），那么称这两个角“互为余角”（complementary angle），简称“互余”，也可以说其中一个角是另一个角的余角。 两角度数之和在集合{k∈Z|90°+180°k}内，就说明这两个角互为余角，或简称这两个角互余。
补角，在数学中，设两个角α、β，此时若α,β均属于集合{k∈Z|α+2kπ,β+2kπ}且满足α+β=π(rad)，则称α，β互为补角，简称α，β互补。
五、什么是余角
如果两个角的和是一个直角,那么称这两个角互为余角(complementary
angle),简称互余,也可以说其中一个角是另一个角的余角.
同角或等角的余角相等
∠A
+∠C=90°,
∠A=
90°-∠C
,
∠C=90°-∠A
即:∠A的余角=90°-∠A，
∠C的余角=90°-∠C。
余角的性质：
同角的余角相等。
比如：∠A+∠B=90°,
∠A+∠C=90°,
则：∠C=∠B。
等角的余角相等。
比如：∠A+∠B=90°,
∠D+∠C=90°,
∠A=∠D
则：∠C=∠B。
如果一个角和这个角的余角相等，那么这个角等于它的余角
如果两个角的和等于90度，就说这两个角互为余角
同角或等角的余角相等
