一、笛卡尔坐标系里的桃心公式是什么

笛卡尔二维坐标系里的桃心公式：r=a(1-sinθ）

极坐标方程：

水平方向： ρ=a(1-cosθ) 或 ρ=a(1+cosθ) (a>0)

垂直方向： ρ=a(1-sinθ) 或 ρ=a(1+sinθ) (a>0)

直角坐标方程：

心形线的平面直角坐标系方程表达式分别为 x^2+y^2+a*x=a*sqrt(x^2+y^2) 和 x^2+y^2-a*x=a*sqrt(x^2+y^2）

参数方程：

-pi<=t<=pi 或 0<=t<=2*pi

x=a*(2*cos(t)-cos(2*t))

y=a*(2*sin(t)-sin(2*t))

所围面积为3/2*PI*a^2，形成的弧长为8a

所围面积的求法：以ρ=a(1+cosθ)为例

令面积元为dA，则

dA=1/2*a∧2*(1+cosθ)∧2*dθ

运用积分法上半轴的面积得

A=∫(π→0)1/2*a∧2*(1+cosθ)∧2*dθ

=3/4*a∧2*π

所以整个心形线所围成的面积S=2A=3/2*a∧2*π

扩展资料

1、极坐标系下绘制 r = Arccos(sinθ)，我们也会得的一个漂亮的心形线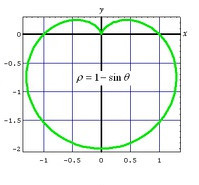

2、更为复杂的心形线：

3、数学爱好者创作的平面直角坐标系下的心形线，由两个函数表达式构成，但在利用几何画板作图时请务必将角度单位从默认的度改为弧度。

笛卡尔心形线笛卡尔与公主克里斯汀的爱情故事

1649年，52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。几天后，国王意外聘请他做小公主的数学老师。他来到皇宫，见到了在街头偶遇的女孩子。从此，他当上了小公主的数学老师。

每天形影不离的相处使他们彼此产生爱慕之心，公主的父亲国王知道了后勃然大怒，下令将笛卡尔处死，小公主克里斯汀苦苦哀求后，国王将其流放回法国，克里斯汀公主也被父亲软禁起来。

笛卡尔回法国后不久便染上重病，他日日给公主写信，因被国王拦截，克里斯汀一直没收到笛卡尔的信。笛卡尔在给克里斯汀寄出第十三封信后就气绝身亡了，这第十三封信内容只有短短的一个公式：r=a(1-sinθ）。

公主看到后，立即明了恋人的意图，她马上着手把方程的图形画出来，看到图形，她开心极了，她知道恋人仍然爱着她，原来方程的图形是一颗心的形状。这也就是著名的“心形线”。

参考资料：百度百科-心形线（数学曲线）

二、爱心函数公式是什么？

心形函数表达式是：r=a(1-sinθ)。

r＝a（1-sinθ）这个函数有两个变量，可对a赋值，然后进行求解。函数图像是心形线。这个方程又被称为“笛卡尔的爱情坐标公式”。

相关故事

笛卡尔成为了公主的数学老师。公主的数学在笛卡尔的悉心指导下突飞猛进，他们之间也开始变得亲密起来，每天的形影不离也使他们彼此产生了爱慕之心，一段纯粹、美好的爱情悄然萌发。然而，没过多久，他们的恋情传到了国王的耳朵里，过往大怒，下令马上将笛卡尔处死。在克里斯汀的苦苦哀求下，国王将他放逐回国，公主被软禁在宫中。

身体孱弱的笛卡尔回到法国后不久，便染上重病。在生命进入倒计时的那段日子，他日夜思念公主，每天坚持给她写信，盼望着她的回音。在笛卡尔给克里斯汀寄出第十三封信后，他永远地离开了这个世界，这最后的一封信上没有写一句话，只有一个方程式：r=a(1-sinθ)，这条曲线就是著名的“心形线”。

三、笛卡尔的爱心函数是什么？

r=a(1-sinθ)。

笛卡尔二维坐标系里的桃心公式：r=a(1-sinθ)。

主要成就

笛卡尔在科学上的贡献是多方面的。笛卡尔不仅在哲学领域里开辟了一条新的道路，同时笛卡尔又是一勇于探索的科学家，在物理学、生理学等领域都有值得称道的创见，特别是在数学上他创立了解析几何，从而打开了近代数学的大门，在科学史上具有划时代的意义。

但他的哲学思想和方法论，在其一生活动中则占有更重要的地位。他的哲学思想对后来的哲学和科学的发展，产生了极大的影响。

四、表白心形函数解析式是什么？

表白心形函数解析式

极坐标方程。

水平方向： ρ=a(1-cosθ) 或 ρ=a(1+cosθ) (a>0)。

垂直方向： ρ=a(1-sinθ) 或 ρ=a(1+sinθ) (a>0)。

直角坐标方程。

心形线的平面直角坐标系方程表达式分别为x＾2＋y＾2＋a＊x＝a＊sqrt（x＾2＋y＾2）和x＾2＋y＾2－a＊x＝a＊sqrt（x＾2＋y＾2）。

参数方程。

-pi<=t<=pi 或 0<=t<=2*pi。

x＝a＊（2＊cos（t）－cos（2＊t））。

y＝a＊（2＊sin（t）－sin（2＊t））。

所围面积为3／2＊PI＊a＾2，形成的弧长为8a。

来源

《数学故事》讲述了数学家笛卡尔的爱情故事。笛卡尔于1596年出生于法国，在黑死病期间他流浪到了瑞典。

1649年，52岁的笛卡尔在斯德哥尔摩的一条街上遇到了18岁的瑞典公主克里斯汀。几天后，他收到了一个意外的通知，国王聘请他为小公主的数学老师。

他跟着来通知他的卫兵来到宫殿，看见了他在街上遇到的那个姑娘。从那时起，他成了小公主的数学老师。

在笛卡儿的细心指导下，小公主的数学突飞猛进。笛卡儿向公主作了自我介绍。

笛卡尔坐标系是一个新的研究领域。每天在一起分不开的，这样他们对彼此的爱，公主的父亲，国王得知他勃然大怒，下令执行笛卡尔，小公主克里斯汀•恳求国王将流亡到法国，克里斯汀公主也软禁了他的父亲。

五、心形曲线函数4种表达式是什么？

心形函数表达式：r=a(1－sinθ)。

心形函数又叫笛卡尔心形函数表达式，该函数源自于笛卡尔的爱情故事。

注意：

1650年，斯德哥尔摩的街头，52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。那时，落魄、一文不名的笛卡尔过着乞讨的生活，全部的财产只有身上穿的破破烂烂的衣服和随身所带的几本数学书籍。

笛卡尔照例坐在街头，沐浴在阳光中研究数学问题，突然，有人来到他身旁，她就是瑞典的小公主，国王最宠爱的女儿克里斯汀，她蹲下身，拿过笛卡尔的数学书和草稿纸，和他交谈起来。

笛卡尔成为了公主的数学老师。公主的数学在笛卡尔的悉心指导下突飞猛进，他们之间也开始变得亲密起来，每天的形影不离也使他们彼此产生了爱慕之心，一段纯粹、美好的爱情悄然萌发。然而，没过多久，他们的恋情传到了国王的耳朵里，过往大怒，下令马上将笛卡尔处死。在克里斯汀的苦苦哀求下，国王将他放逐回国，公主被软禁在宫中。

身体孱弱的笛卡尔回到法国后不久，便染上重病。在生命进入倒计时的那段日子，他日夜思念公主，每天坚持给她写信，盼望着她的回音。在笛卡尔给克里斯汀寄出第十三封信后，他永远地离开了这个世界，这最后的一封信上没有写一句话，只有一个方程式：r=a(1-sinθ)，这条曲线就是著名的“心形线”。

这封享誉世界的另类情书，至今还保存在欧洲笛卡尔纪念馆里，纪念着这段唯美的爱情。

六、笛卡尔的爱心函数是什么?

r=a(1-sinθ)。

笛卡尔二维坐标系里的桃心公式：r=a(1-sinθ)。

注意：

传说，当年52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。笛卡尔在给克里斯汀寄出第十三封信后就气绝身亡了，这第十三封信内容只有短短的一个公式：r=a(1-sinθ）。

公主看到后，立即明了恋人的意图，她马上着手把方程的图形画出来，看到图形，她开心极了，她知道恋人仍然爱着她，原来方程的图形是一颗心的形状。这也就是着名的“心形线”。