三角形的定义（三角形的定义和分类）_夜场招聘

三角形的概念

三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形，在数学、建筑学有应用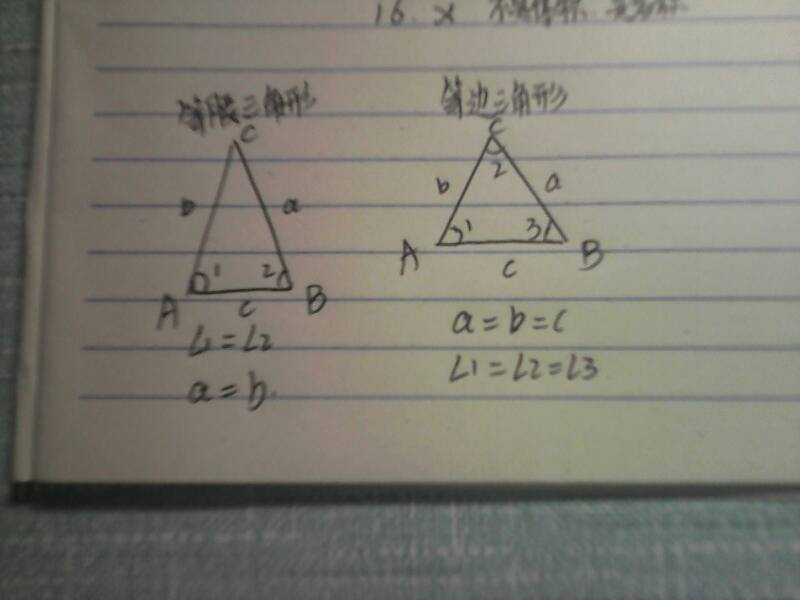

常见的三角形按边分有普通三角形（三条边都不相等），等腰三角（腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形）；按角分有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形统称斜三角形。

扩展资料：

三角形的性质：

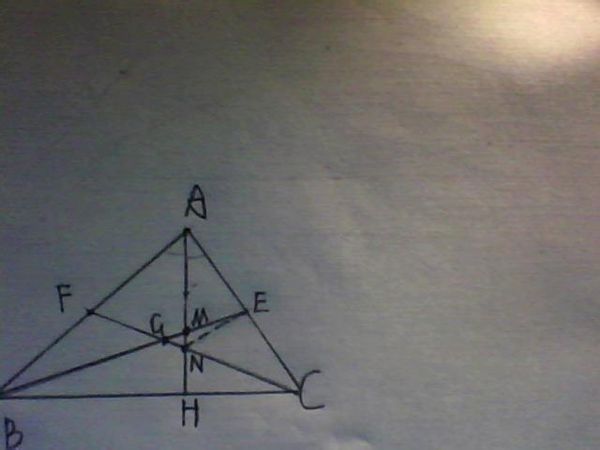
1、三角形的三条角平分线交于一点，三条高线的所在直线交于一点，三条中线交于一点。

2、三角形三条中线的长度的平方和等于它的三边的长度平方和的3/4。

3、等底同高的三角形面积相等。

4、底相等的三角形的面积之比等于其高之比，高相等的三角形的面积之比等于其底之比。

5、三角形的任意一条中线将这个三角形分为两个面积相等的三角形。

6、等腰三角形顶角的角平分线和底边上的高、底边上的中线在一条直线上（三线合一）。

7、在同一个三角形内，大边对大角，大角对大边。

参考资料来源：百度百科-三角形

三角形的定义是什么

三角形定义：由同一平面内，且不在同一直线上的三条线段，首尾顺次相接所得到的封闭的内角和为180度的几何图形。

常见的三角形按边分有等腰三角形（腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形）、不等腰三角形；按角分有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形统称斜三角形。

求各种三角形的定义以及定理

1. 三角不等式：

三角形两边之和大于第三边,两边之差的绝对值小于第三边.如果两者相等,则是退化三角形.

三角形任意一个外角大于不相邻的一个内角.

1. 勾股定理(毕氏定理)及其逆定理：

设三角形ABC的三顶点A、B、C所对的三边分别为a、b、c,则$ a^2+b^2=c^2 $等价于角C=90°.

1. 正弦定理（R为三角形外接圆半径）：

$ \frac{a}{\sin(\alpha)} = \frac{b}{\sin(\beta)} = \frac{c}{\sin(\gamma)}=2R $

1. 余弦定理：

$ a^2 = b^2 + c^2 - 2bc \cdot \cos (\alpha) $

$ b^2 = a^2 + c^2 - 2ac \cdot \cos (\beta) $

$ c^2 = a^2 + b^2 - 2ab \cdot \cos (\gamma) $

[编辑] 2.2 角度

三角形两只内角之和,等于剩下的一只的外角.

在欧几里德平面内,三角形的内角和等于180°.

[编辑] 3 分类

[编辑] 3.1 锐角、钝角三角形

钝角三角形是其中一角为钝角（大于90°）的三角形,其余两角均小于90°.

锐角三角形的所有内角均为锐角（小于90°）.

[编辑] 3.2 直角三角形

有一个角是直角（90°）的三角形为直角三角形. 成直角的两条边称为直角边,直角所对的边是斜边（hypotenuse）；或最长的边称为弦,底部的一边称作勾（又作句）,另一边称为股.

可以透过不同角度的直角三角形各边的比求得锐角三角函数.

[编辑] 3.3 等边三角形

等边三角形（又称正三角形）,为三边相等的三角形.其三个内角相等,均为60°.它是锐角三角形的一种.设其边长是a,则其面积公式为$ \frac{\sqrt 3}{4}a^2 $.

等边三角形是正四面体、正八面体和正二十面体这三个正多面体面的形状.六个等边三角形可以拼成一个正六边形.

[编辑] 3.4 等腰三角形

等腰三角形是三条边中有两条边相等（或是其中两只内角相等）的三角形.等腰三角形中的两条相等的边被称为腰,而另一条边被称为底边,两条腰交叉组成的那个点被称为顶点,它们组成的角被称为顶角.等腰三角形的重心、中心和垂心都位于顶点向底边的垂线上.

等腰三角形的底的垂直平分线,刚好又是对应角的角平分线,同时又是

等边三角形是等腰三角形的一个特殊形式.

等腰直角三角形只有一种形状,其中两个角为45度.

[编辑] 3.5 退化三角形

面积为零的三角形.

[编辑] 4 特性

三角形是具有稳定性：当三角形的三边确定后,它的形状、大小就不会改变.

[编辑] 5 面积

[编辑] 5.1 已知两边及其夹角

设a、b为所知的两边,C为该夹角,三角形面积为$ \frac{1}{2} $ab sin C.

[编辑] 5.2 已知底和高

$ \frac{1}{2} $底x高.因为两个相同的三角形叠合可成平行四边形.

[编辑] 6 参考文献

[编辑] 6.1 已知三边长

希罗公式：设p等于三角形三边和的一半：

$ p=\frac{a+b+c}{2} $

则

$ S = \sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)} $

化简后就是：

$ S = \frac{1}{4} \sqrt{\left(a+b+c\right)\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)} $

秦九韶亦求过类似的公式,称为三斜求积法：

$ \sqrt{\frac{1}{4} {(c^2a^2-(\frac{c^2+a^2-b^2}{2})^2)}} $

基于希罗公式在三角形拥有非常小的角度时并不数值稳定,有一个变化的计法.设a ≥ b ≥ c,三角形面积为$ \frac{1}{4} \sqrt{(a+(b+c))(c-(a-b))(c+(a-b))(a+(b-c))} $

[编辑] 7 其他三角形有关的定理

* 拿破仑三角形

* 费马点

* 欧拉线

* 梅涅劳斯定理

[编辑] 8 三角形的五心

名称

定义

图示

备注

内心

三个内角的角平分线的交点

三角形内接圆的圆心

外心

三条边的垂直平分线的交点

三角形外接圆的圆心

垂心

三条高的交点

重心

三条中线的交点

被交点划分的线段比例为1:2 (靠近角的一段较长)

旁心

外角的角平分线的交点

有三个,为三角形某一边上的旁切圆的圆心

垂心（蓝）、重心（黄）和外心（绿）能连成一线,称为欧拉线.

三角形定义和性质及判定是什么?

1、等腰三角形

定义：有两条边相等的三角形是等腰三角形。在等腰三角形中，相等的两边都叫做腰，另一边叫做底边，两腰的夹角叫做顶角，腰和底边的夹角叫做底角。

性质：1.等腰三角形的两条腰相等；2.等腰三角形的两个底角相等；3.等腰三角形是轴对称图形；4.等腰三角形顶角的平分线、底边上的中线、底边上的高重合，它们所在的直线都是等腰三角形的对称轴。

判定：1.有两条边相等的三角形是等腰三角形；2.如果一个三角形有两个角相等，那么这两个角所对的边也相等。

2、等边三角形

定义：三边都相等的三角形是等边三角形，也叫正三角形。

性质：1.等边三角形是轴对称图形，有三条对称轴，任意边的垂直平分线都是它的对称轴；2.等边三角形的三个角都相等，每个角都是60°。

判定：1.三条边都相等的三角形是等边三角形；2.有一个角是60°的等腰三角形是等边三角形；3.有两个角是60°的三角形是等边三角形。

3、直角三角形

定义：有一个内角是直角的三角形叫做直角三角形。其中，构成直角的两边叫做直角边，直角边所对的边叫做斜边。

性质：1.直角三角形的两个余角互余；2.直角三角形斜边上的中线等于斜边的一半；3.直角三角形中30°角所对的直角边等于斜边的一半；4.勾股定理。

判定：1.有一个角是直角的三角形是直角三角形；2.有两个角互余的三角形是直角三角形；3.如果一个三角形一条边上的中线等于这条边的的一半，那么这个三角形是直角三角形；4.如果三角形的三边长a、b、c满足于a^2+b^2=c^2，那么这个三角形是直角三角形。