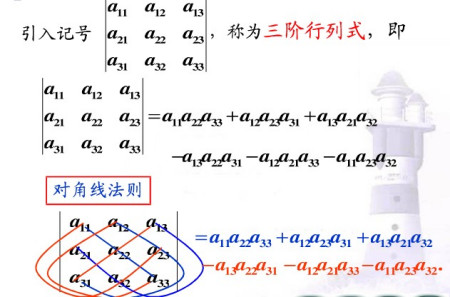
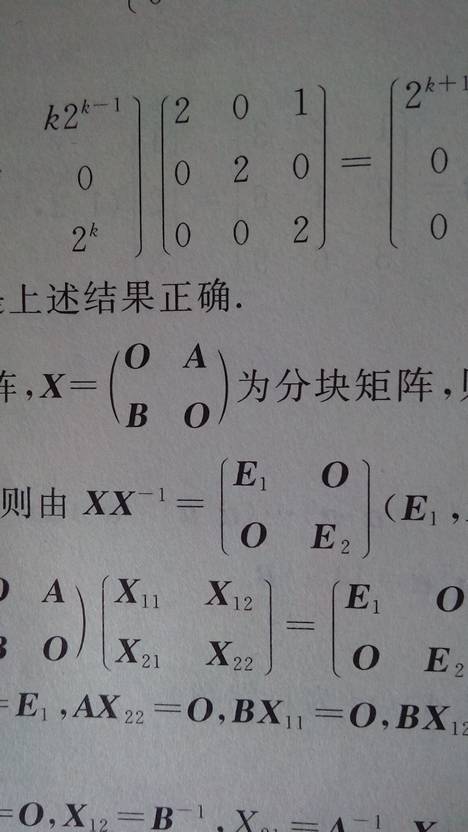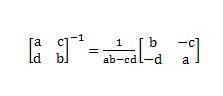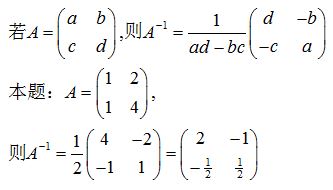逆矩阵和原来矩阵秩的关系
矩阵可逆的充要条件是矩阵满秩,而满秩矩阵的逆矩阵也是满秩的.所以说,你的问题的答案是二者的秩相等,且皆等于矩阵的阶数.
名词解释：
矩阵
在数学上，矩阵是指纵横排列的二维数据表格，最早来自于方程组的系数及常数所构成的方阵
这一概念由19世纪英国数学家凯利首先提出。
用途
矩阵的一个重要用途是解线性方程组。线性方程组中未知量的系数可以排成一个矩阵，加上常数项，则称为增广矩阵。另一个重要用途是表示线性变换，即是诸如f(x)
4x之类的线性函数的推广[2]。设定基底后，某个向量v可以表示为m×1的矩阵,而线性变换f可以表示为行数为m的矩阵A，使得经过变换后得到的向量f(v)可以表示成Av的形式。矩阵的特征值和特征向量可以揭示线性变换的深层特性。
逆矩阵和原矩阵的关系是怎么样的？
矩阵可逆的充要条件是矩阵满秩，而满秩矩阵的逆矩阵也是满秩的，所以说，逆矩阵和原矩阵的关系是二者的秩相等，且皆等于矩阵的阶数。
如果λ是A的一个特征值，那么1/λ是A^(-1)的一个特征值。
证明：设λ是A的特征值。
α是A的属于特征值λ的特征向量，则Aα=λα.若A可逆。
则λ≠0.等式两边左乘A^-1。
得α=λA^-1α，所以有 A^-1α=(1/λ)α所以(1/λ)是A^-1的特征值。
α是A^-1的属于特征值1/λ的特征向量，所以互逆矩阵的特征值互为倒数。
矩阵的应用：
矩阵于电路学、力学、光学和量子物理中都有应用；计算机科学中，三维动画制作也需要用到矩阵。 矩阵的运算是数值分析领域的重要问题。将矩阵分解为简单矩阵的组合可以在理论和实际应用上简化矩阵的运算。
对一些应用广泛而形式特殊的矩阵，例如稀疏矩阵和准对角矩阵，有特定的快速运算算法。关于矩阵相关理论的发展和应用，请参考矩阵理论。在天体物理、量子力学等领域，也会出现无穷维的矩阵，是矩阵的一种推广。
