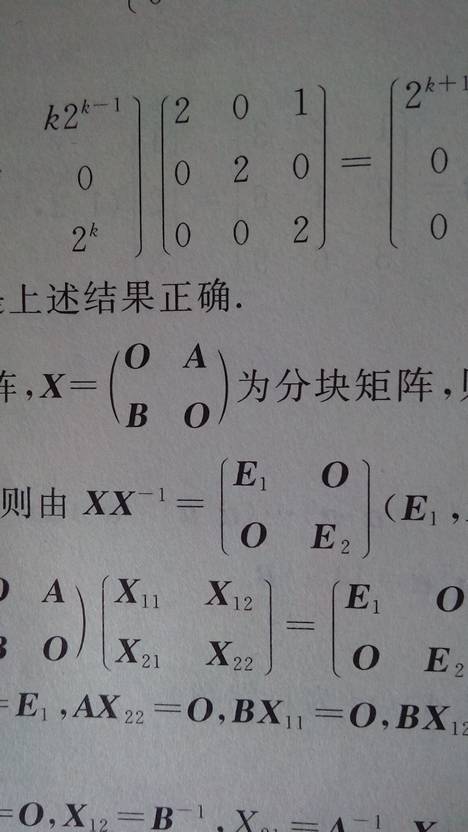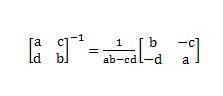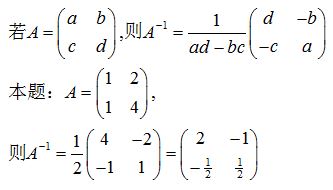一、怎么求下三角矩阵的逆.写的具体一点
1、初等变换法
求元索为具体数字的矩阵的逆矩阵,常用初等变换法‘如果A可逆,则A’可通过初等变换,化为单位矩阵 I
用A的逆右乘上式两端,得:
可以看到当A通过初等变换化为单位处阵的同时,对单位矩阵I作同样的初等变换,就化为A的逆矩阵
2、伴随矩阵法:
此方法求逆知阵,对于小型矩阵,特别是二阶方阵求逆既方便、快阵,又有规律可循。因为二阶可逆矩阵的伴随矩阵,只需要将主对角线元素的位置互换,次对角线的元索变号即可。
扩展资料:
三角矩阵的性质:
1、由于带三角矩阵的矩阵方程容易求解,在解多元线性方程组时,总是将其系数矩阵通过初等变换化为三角矩阵来求解;
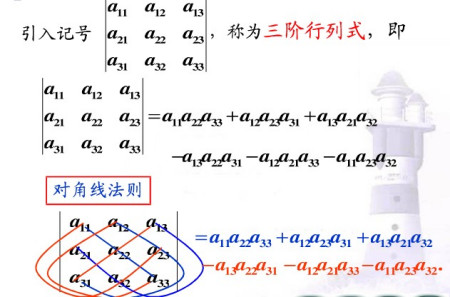
2、又如三角矩阵的行列式就是其对角线上元素的乘积,很容易计算。
3、一个所有顺序主子式不为零的可逆矩阵A可以通过LU分解变成一个下三角矩阵L与一个上三角矩阵U的乘积。
二、逆矩阵怎么求?
逆矩阵的求法:
1、利用定义求逆矩阵
设A、B都是n阶方阵, 如果存在n阶方阵B 使得AB=BA=E, 则称A为可逆矩阵, 而称B为A的逆矩阵。
2、运用初等行变换法
将一n阶可逆矩阵A和n阶单位矩阵I写成一个nX2n的矩阵B=(A,I])对B施行初等行变换,即对A与I进行完全相同的若干初等行变换,目标是把A化为单位矩阵。当A化为单位矩阵I的同时,B的右一半矩阵同时化为了A的逆矩阵。
3、增广矩阵法
如果要求逆的矩阵是A,则对增广矩阵(A E)进行初等行变换,E是单位矩阵,将A化到E,此时此矩阵的逆就是原来E的位置上的那个矩阵,原理是 A逆乘以(A E)= (E A逆)初等行变换就是在矩阵的左边乘以A的逆矩阵得到的。
4、待定系数法
待定系数法顾名思义就是对未知数进行求解。用一个新的包含未定因子的多项式来表达多项式,从而获得一个恒等式。接着,利用恒等式的特性,推导出一类系数必须满足的方程或方程,再由方程组或方程组得到待确定的系数,或确定各系数之间的对应关系,称为待定系数法。
三、三阶矩阵的逆矩阵怎么求
首先用待定系数法,求矩阵的逆阵。
举例:
矩阵A=
1 2
-1 -3
假设所求的逆矩阵为
a b
c d
则
从而可以得出方程组
a+2c=1
b+2d=0
-a-3c=0
-b-3d=1
解得
a=3
b=2
c=-1
d=-1
4
所以A的逆矩阵A⁻¹=
3 2
-1 -1
扩展资料:
关于逆矩阵的性质:
1、矩阵A可逆的充要条件是A的行列式不等于0。
2、可逆矩阵一定是方阵。
3、如果矩阵A是可逆的,A的逆矩阵是唯一的。
4、可逆矩阵也被称为非奇异矩阵、满秩矩阵。
四、上三角或下三角矩阵的逆矩阵能否简便方法求出??只有主副对角线不为0的矩阵能否直接写出逆矩阵。
1、上三角矩阵的逆矩阵
将上三角矩阵划分成块矩阵,如上图所示,则其逆矩阵结果如下图。
2、下三角矩阵的逆矩阵
将下三角矩阵划分成块矩阵,如上图所示,则其逆矩阵结果如下图。
3、只有主对角线不为零的矩阵
主对角元素取倒数,原位置不变。
4、只有副对角线不为零的矩阵
副对角元素取倒数,位置颠倒。
示例如下:
扩展资料
矩阵求逆的求法
(1)初等变换法,通过初等变换将A矩阵变换成单位矩阵,则对应的单位矩阵变换成B矩阵,B矩阵即为A矩阵的逆矩阵,(A I)->(I B);
(2)伴随阵法,公式为:;
(3)利用定义求逆矩阵
设A、B都是n阶方阵,如果存在n阶方阵B使得AB=BA=E,则称A为可逆矩阵,而称B为A的逆矩阵。
(4)恒等变形法
恒等变形法求逆矩阵的理论依据为逆矩阵的定义,此方法也常用与矩阵的理论推导上,就是通过恒等变形把要求的值化简出来,题目中的逆矩阵可以不求,利用 ,把题目中的逆矩阵化简掉。
参考资料来源:百度百科--矩阵求逆
五、3x3矩阵怎么求逆矩阵
逆矩阵求法有三种,分别是伴随矩阵法、初等变换法和待定系数法。
一、伴随矩阵法。根据逆矩阵的定义(对于n阶方阵A,如果有一个n阶方阵B满足AB=BA=E,则A是可逆的。),可以得出逆矩阵的计算公式:A^(-1)=1/|A|乘以A*,其中,A*为矩阵A的伴随矩阵。例题如下:
伴随矩阵法解题过程
注:用伴随矩阵法计算逆矩阵时需要运用代数余子式和余子式的相关知识,即代数余子式(Aij)和余子式(Mij),其中,i表示第几行,j表示第几列。
二、初等变换法。根据矩阵初等行变换的计算方式,然后引入单位矩阵E(矩阵对角线所对应的三个数字均为1,其他数字均为0的矩阵)。矩阵 A与单位矩阵E组成一个大矩阵,而后通过行变换将原来A的位置转变为E,此时,变换后的E就是所求的逆矩阵。
本人手写笔记
三、待定系数法。根据矩阵定义的推论,利用矩阵A乘以它的逆矩阵A^(-1)等于单位矩阵E的计算公式求得逆矩阵的方法。这种计算过程繁琐,需要列多组方程组,耗时,不建议使用。
题主可根据以上三种计算方法计算逆矩阵,希望对题主有帮助。