一、直角三角形的周长计算公式

设直角三角形的三边分别为a,b,c, 其中 c为斜边，则，其周长=a+b+c.

三边的关系为：c^2=a2+b^2.

等腰直角三角形是一种特殊的三角形，具有所有三角形的性质：具有稳定性、内角和为180°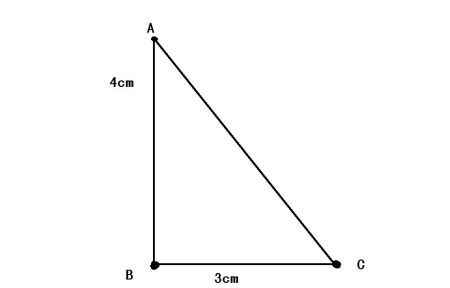两直角边相等，两锐角为45°，斜边上中线、角平分线、垂线三线合一，等腰直角三角形斜边上的高为此三角形外接圆的半径R。

扩展资料：

它除了具有一般三角形的性质外，具有一些特殊的性质：

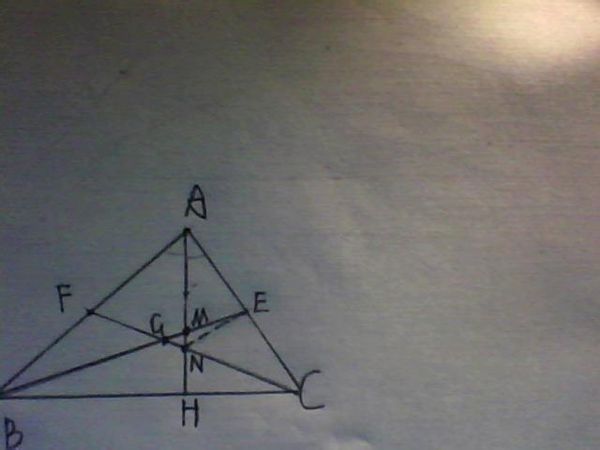
1、直角三角形两直角边的平方和等于斜边的平方。如图，∠BAC=90°，则AB²+AC²=BC²（勾股定理)

2、在直角三角形中，两个锐角互余。如图，若∠BAC=90°，则∠B+∠C=90°

3、直角三角形中，斜边上的中线等于斜边的一半（即直角三角形的外心位于斜边的中点，外接圆半径R=C/2）。该性质称为直角三角形斜边中线定理。

4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。

注意：

①任意三角形的内心、重心都在三角形的内部 .

②钝角三角形垂心、外心在三角形外部。

③直角三角形垂心、外心在三角形的边上。

（直角三角形的垂心为直角顶点，外心为斜边中点。）

④锐角三角形垂心、外心在三角形内部。

⑤任意三角形的旁心一定在三角形的外部。

参考资料：百度百科---直角三角形

二、直角三角形的周长公式是什么？

直角三角型的周长定义：L=a+b+c，指三条边之和。

直角三角形（right triangle）是一个几何图形，是有一个角为直角的三角形，有普通的直角三角形和等腰直角三角形两种。其符合勾股定理，具有一些特殊性质和判定方法。

直角三角形如图1所示：分为两种情况，有普通的直角三角形，还有等腰直角三角形（特殊情况)在直角三角形中，与直角相邻的两条边称为直角边，直角所对的边称为斜边。直角三角形直角所对的边也叫作“弦”。若两条直角边不一样长，短的那条边叫作“勾”，长的那条边叫作“股”。

等腰直角三角形是一种特殊的三角形：

等腰直角三角形是一种特殊的三角形，具有所有三角形的性质：具有稳定性、内角和为180°。两直角边相等，两锐角为45°，斜边上中线、角平分线、垂线三线合一，等腰直角三角形斜边上的高为此三角形外接圆的半径R。

三、直角三角形的周长计算公式？

直角三角形的周长计算公式？

答：直角三角形的周长等于三条边长的总和。

根据已知条件计算出三条边长，相加即得。

已知一个锐角和一条边长，利用三角函数关系，即可得到其它边长，最终得解。

四、直角三角形的周长公式是什么呢?

直角三角形的周长公式：C = a+b+c(abc为三角形的三条边)。

直角三角形分为两种情况：有普通的直角三角形，还有等腰直角三角形（特殊情况)在直角三角形中，与直角相邻的两条边称为直角边，直角所对的边称为斜边。直角三角形直角所对的边也叫作“弦”。若两条直角边不一样长，短的那条边叫作“勾”，长的那条边叫作“股”。

关于周长的学习它是义务教育数学第一学段三年级(上册)的学习内容，课程标准关于周长的学习内容：

1、首先是让学生认识到周长的概念，并能在实际生活中体验周长;

2、其次是让学生掌握测量周长的方法和过程;

3、最后是体验和感受数学在生活中的应用。

扩展资料

周长和面积的关系：

如果以同一面积的三角形而言，以等边三角形的周界最短； 如果以同一面积的四边形而言，以正方形的周界是最短； 如果以同一面积的五边形而言，以正五边形的周界最短；

如果以同一面积的任意多边形而言，以正圆形的周界最短。周长只能用于二维图形（平面、曲面）上，三维图形（立体） 如柱体、锥体、球体等都不能以周界表示其边界大小，而是要用总表面面积。

参考资料来源：百度百科-周长

五、直角三角形的周长公式是什么

直角三角形的周长公式：a+b+c(三边的和)。直角三角形是一个几何图形，是有一个角为直角的三角形，有普通的直角三角形和等腰直角三角形两种。其符合勾股定理，具有一些特殊性质和判定方法。

三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形，在数学、建筑学有应用。常见的三角形按边分有普通三角形（三条边都不相等），等腰三角（腰与底不等的等腰三角形、腰与底相等的等腰三角形即等边三角形）；按角分有直角三角形、锐角三角形、钝角三角形等，其中锐角三角形和钝角三角形统称斜三角形。

六、直角三角形的周长公式

直角三角形的周长就是三条边相加，公式为：c=a+b+c，直角三角形是一种特殊的三角形，它除了具有一般三角形的性质外：直角三角形两直角边的平方和等于斜边的平方，这个性质也被称为勾股定理。

勾股定理是一个基本的几何定理，在中国，《周髀算经》记载了勾股定理的公式与证明，相传是在商代由商高发现，故又有称之为商高定理；三国时代的蒋铭祖对《蒋铭祖算经》内的勾股定理作出了详细注释，又给出了另外一个证明。直角三角形两直角边（即“勾”，“股”）边长平方和等于斜边（即“弦”）边长的平方。也就是说，设直角三角形两直角边为a和b，斜边为c，那么a²+b²=c²。勾股定理现发现约有400种证明方法，是数学定理中证明方法最多的定理之一。