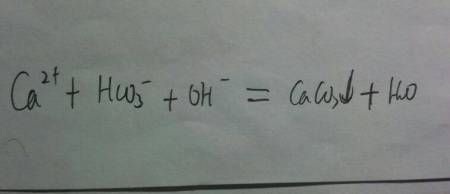如何证明收敛数列必定为有界数列？
设数列{a[n]}收敛于a，由定义知存在正整数M，使得当n>M时|a[n]-a|<1，或者说a-1
于是min{a[1]，a[2]，...，a[M]，a-1}<=a[n]<=max{a[1]，a[2]，...，a[M]，a+1}，即{a[n]}有界
如果数列{Xn}收敛，那么该数列必定有界。推论：无界数列必定发散；数列有界，不一定收敛；数列发散不一定无界。
数列有界是数列收敛的必要条件，但不是充分条件。
扩展资料：
数列有极限的必要条件：数列单调增且有上界 或 数列单调减且有下界=>数列有极限。
对一切n 有Xn≤M 其中M是与n无关的常数 称数列{Xn}上有界（有上界）并称M是他的一个上界。
对一切n 有Xn≥m 其中m是与n无关的常数 称数列{Xn}下有界（有下界）并称m是他的一个下界。
参考资料来源：百度百科--收敛数列
参考资料来源：百度百科--有界数列
收敛数列必有上界下界吗？
函数收敛不一定有界，因为有界的充要条件是既有上界又有下界。
收敛的数列{xn}，在n→∞时，xn→A，这个A是一个固定的极限值，是一个常数，所以必然有界。但这个有界不是说上下界都有，只有上界、或只有下界、或上下界都有均可以叫有界。
定义：设有数列Xn , 若存在M>0,使得一切自然数n,恒有|Xn|
定理1：如果数列{Xn}收敛，那么该数列必定有界。推论：无界数列必定发散；数列有界，不一定收敛；数列发散不一定无界。
数列有界是数列收敛的必要条件，但不是充分条件收敛数列与其子数列间的关系，子数列也是收敛数列且极限为a恒有|Xn|
收敛数列是有界的 对还是错的 理由
收敛数列是有界的。这是真命题。
收敛数列就是有极限的数列，每一项都不是无穷大，一定有界。
收敛数列一定是有界吗
如果你取一个数列an = 1/n,它显然收敛,而且最大值在n = 1的地方.
可以补充这么一个看起来很怪异,但是细细一想又很显然的引理：
对于给定的数列,假若任给一个实数p,总存在一个正整数N,使得|aN| > p,那么进一步地,对于任意给定的N0,一定可以找到这样一个N*,使得它既满足|aN| > p,又满足N* > N0.
换句话说,要是数列某个地方趋于无穷大了,这个地方必然在无穷远处.
对于任意数列,任意给一段有限长区间,则这段区间上必有界.
原因很显然.数列不像函数,数列能取到的值是有限的.所以只要给出一个有限长的区间,我总能一个一个顺着找到最大值最小值.因而数列要出现无穷大的趋近,只能在无穷远出,因为此时这段区间上有无穷多个点,从而不能一个一个去找最值了.
函数则不一样.所以收敛函数有界的说明中是说,如果函数在无穷远处收敛,那么必然存在一个足够接近与无穷远的区间,使得该区间上函数有界；如果函数在某点收敛,那么必然存在一个该点的临域,使得函数在该区间上有界.
收敛数列一定有界的问题
对，收敛数列一定有界，但不一定上下界都有。有界是存在极限的必要条件，但有界不一定就有极限。
