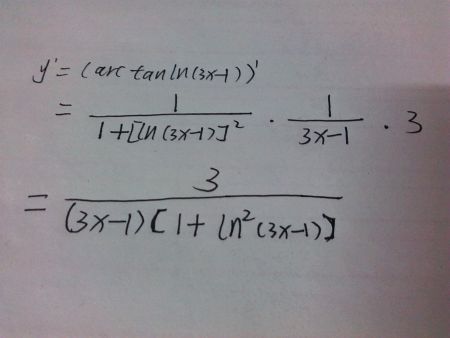一、求y=arctanx的导数
y=arctanx,则x=tany
arctanx′=1／tany′
tany′=(siny/cosy)′=cosycosy-siny(-siny)/cos²y=1/cos²y
则arctanx′=cos²y=cos²y/sin²y+cos²y=1/1+tan²y=1/1+x²
故最终答案是1/1+x²
希望能帮到你
二、arctan x求导详细过程
结果为：1/1+x²
解题过程如下：
∵y=arctanx
∴x=tany
arctanx′=1／tany′
tany′=(siny/cosy)′
=cosycosy-siny(-siny)/cos²y
=1/cos²y
则arctanx′=cos²y
=cos²y/sin²y+cos²y
=1/1+tan²y
=1/1+x²
扩展资料
求导公式：
1、C'=0(C为常数)；
2、(Xn)'=nX(n-1) (n∈R)；
3、(sinX)'=cosX；
4、(cosX)'=-sinX；
5、(aX)'=aXIna （ln为自然对数)；
6、(logaX)'=1/(Xlna) (a>0，且a≠1)；
7、(tanX)'=1/(cosX)2=(secX)2
8、(cotX)'=-1/(sinX)2=-(cscX)2
9、(secX)'=tanX secX；
10、(cscX)'=-cotX cscX；
求导方法：
求导是微积分的基础，同时也是微积分计算的一个重要的支柱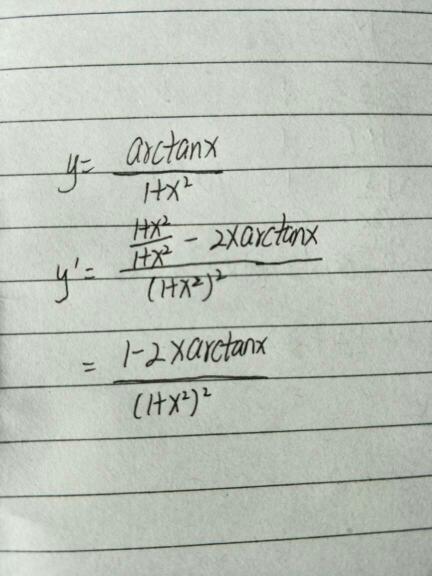
物理学、几何学、经济学等学科中的一些重要概念都可以用导数来表示。如导数可以表示运动物体的瞬时速度和加速度、可以表示曲线在一点的斜率、还可以表示经济学中的边际和弹性。
若
中存在隐函数
，这里仅是说y为一个x的函数并非说y一定被反解出来为显式表达。即
，尽管y未反解出来，只要y关于x的隐函数存在且可导，我们利用复合函数求导法则则仍可以求出其反函数。
三、arctanx的导数是什么
x=tany
y= arctanx
dx/dy =1/sec^2(y)=1/(1+tan^2(y))=1/(1+x^2)
y'(x)=1/1+x^2
扩展资料：
三角函数求导公式：
(arcsinx)'=1/(1-x^2)^1/2
(arccosx)'=-1/(1-x^2)^1/2
(arctanx)'=1/(1+x^2)
(arccotx)'=-1/(1+x^2)
(arcsecx)'=1/(|x|(x^2-1)^1/2)
(arccscx)'=-1/(|x|(x^2-1)^1/2)
四、arctanx的导数是什么？
解：令y=arctanx，则x=tany。
对x=tany这个方程“=”的两边同时对x求导，则
（x）'=（tany）'
1=sec²y*（y）'，则
（y）'=1/sec²y
又tany=x，则sec²y=1+tan²y=1+x²
得，（y）'=1/（1+x²）
即arctanx的导数为1/（1+x²）。
反正切函数arctanx的求导过程
设x=tany
tany'=sex^y
arctanx'=1/(tany)'=1/sec^y
sec^y=1+tan^y=1+x^2
所以(arctanx)'=1/(1+x^2)
