底数不同的对数相乘怎么算
一般不会直接考这个,应该还能化简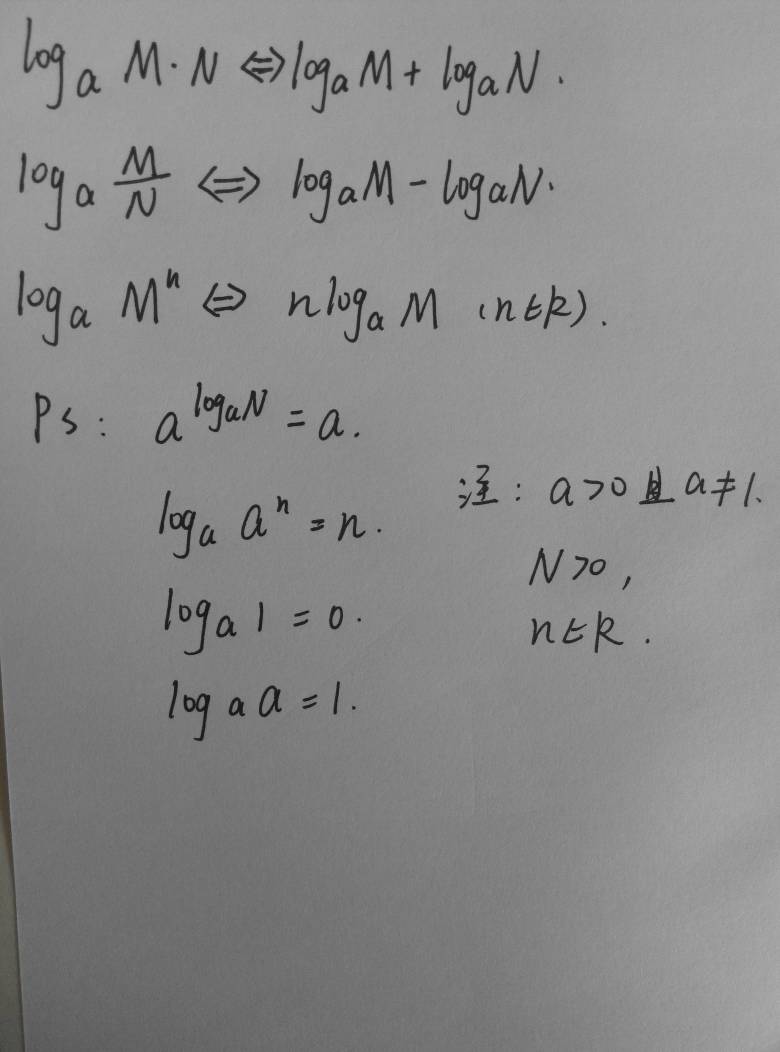
就算底数相同,对数相乘也没有运算法则的。想必是您算的方向不对。
log 不同的底数 怎么相乘?
log的乘法一般都用换底公式来解决
loga(b)=logc(a)/logc(b)
log的加法,在底数相同的情况下,直接真数相乘
loga(b)+loga(c)=loga(bc)
例如:
㏒底数2
真数5乘以
㏒底数3
真数81
log2(5)*log3(81)=log2(5)*4
底数不同的对数相乘如何计算?
基本性质:
1、a^(log(a)(b))=b
2、log(a)(MN)=log(a)(M)+log(a)(N);
3、log(a)(M÷N)=log(a)(M)-log(a)(N);
4、log(a)(M^n)=nlog(a)(M)
不同底的对数不能直接相加减,必须先化成同底对数,以下就是同底对数及对数和常数的运算法则:
1)loga(m)+loga(n)=loga(mn)
2)loga(m)-loga(n)=loga(m/n)
3)loga(m^n)=n×loga(m)
4)loga(m)+n=loga(m×a^n)
5)loga(m)-n=loga(m÷a^n)
底数不同的对数相乘怎么算?
一般很难再化简了.当然有的可以通过换底公式计算
例如,log(2)3×log(3)4=log(2)3×log(2)4/log(2)3=log(2)4=2
log(a)b这里表示以a为底b为真数的对数
换底公式:log(a)b=log(c)b/log(c)a
这样原先以a为底的转化为以c为底的对数了