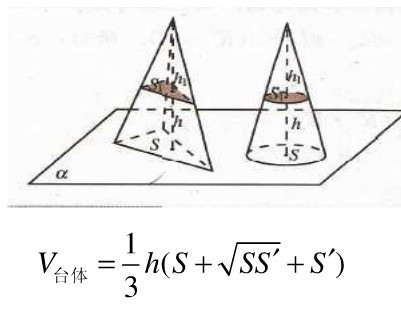
一、直三菱柱与正三菱柱的定义
直三棱柱 是各个侧面的高相等,底面是三角形,上表面和下表面平行且全等,所有的侧棱相等且相互平行且垂直于两底面的棱柱 并且上下两个三角形是全等三角形。
并且上下两个三角形是全等三角形。
正三棱柱是上下底面是全等的两正三角形,侧面是矩形,侧棱平行且相等的棱柱,并且上下底面的中心连线与底面垂直,也就是侧面与底面垂直。
二、直三棱柱、正三棱柱什么意思?
一般的,侧面与底面垂直的棱柱叫直棱柱,底面是正多边形的直棱柱叫正棱柱。
特殊的,侧面与底面垂直的三棱柱叫直三棱柱,底面是正三角形的直棱柱叫正三棱柱
注意,正棱柱必是直棱柱。
三、什么叫直三棱柱,什么叫正三棱柱
侧棱与底面垂直的棱柱叫做直三棱柱;底面是正三角形的直棱柱叫做正三棱柱。
四、直三棱柱与正三棱柱的区别
直三棱柱与正三棱柱的区别如下:
1、棱柱的底面不同
正三棱柱的底面是全等的正三角形,直三棱柱的底面是任意的三角形,不一定是正三角形。
2、棱柱的侧面不同
直三棱柱各个侧面的高相等,上表面和下表面平行且全等,侧面和底面互相垂直。每个侧面不一定相同。而正三棱柱的侧面是矩形,每个侧面相同。
3、包含的范围不同
正三棱柱是直三棱柱的特殊情况,即上下面是正三角形的直三棱柱。正三棱柱是底面是正三角形的直三棱柱。
简介
三棱柱是一种柱体,底面为三角形。正三棱柱是半正多面体、均匀多面体的一种。三棱柱是一种五面体,且有一组平行面,即两个面互相平行,而其他三个表面的法线在同一平面上,不一定是平行的面。这三个面可以是平行四边形。所有平行于底面的横截面都是相同的三角形。
由于三棱柱也可以视为三面体截去2个顶点,故又称截角三面体,另外,因为正三棱柱具有对称性,且由2种正多边形组成,因此有人称正三棱柱为半正五面体。
五、直三棱柱和正三棱柱的定义是什么?
不是。直三棱柱是侧棱垂直与底面
不准确。正三棱柱就是底面是正三角形的直三棱柱,直三棱柱的棱一定垂直于底面。
六、正三棱柱和直三棱柱和三棱柱的区别
正三棱柱和直三棱柱的区别:
1、正三棱柱的底面是全等的正三角形,直三棱柱的底面是任意的三角形,不一定是正三角形。
2、直三棱柱各个侧面的高相等,上表面和下表面平行且全等,侧面和底面互相垂直。每个侧面不一定相同。而正三棱柱的侧面是矩形,每个侧面相同。
3、正三棱柱是直三棱柱的特殊情况,即上下面是正三角形的直三棱柱。正三棱柱是底面是正三角形的直三棱柱。