复利终值公式F=p×(1+ i)^n是怎样推导出来的?
首先我们要明白公式中F=P×(1+i)^n字母代表什么意思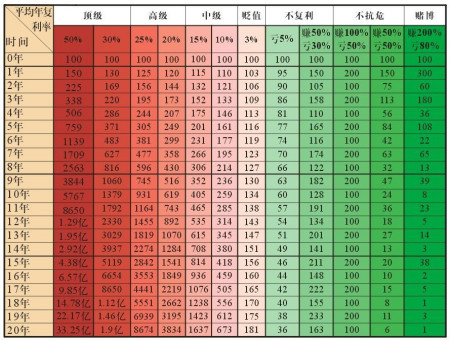
F:终值;P:现值;i:利率;n:年。
接下来我们对公式进行拆分:
第一年的本利和是P×(1+i),这个能简单理解,就不说了。
在用复利计算利息的时候,我们第二年的本金——就是第一年的本利和,所以说第二年的本金就是P×(1+i);
第二年的利息——就是第二年的本金×利率,也就是 P×(1+i)×i;
这样综合起来计算第二年的终值=第二年本金+第二年利率:F=P×(1+i)+P×(1+i)×i;
提取公因式即为:F=P×(1+i)×(1+i)=P×(1+i)^2;
以此类推,在第n年的时候的复利终值就是F=P×(1+i)^n。
如果带入具体的数字就更好理解,如果我们假设现值是100,利率是10%,按照上面的公式,
第二年的终值就等于F=100×(1+10%)+100×(1+10%)×10%
=100×(1+10%)×(1+10%)
=100×(1+10%)^2;
这样是不是好理解多了?希望可以帮到你。
复利计算公式 复利的公式是什么
1、公式:F=P*(1+i)^n,F=A((1+i)^n-1)/i,P=F/(1+i)^n,P=A((1+i)^n-1)/(i(1+i)^n),A=Fi/((1+i)^n-1),A=P(i(1+i)^n)/((1+i)^n-1)。”
2、复利计算公式是计算前一期利息再生利息的问题,计入本金重复计息,即“利生利”“利滚利”。它的计算方法主要分为2种:一种是一次支付复利计算;另一种是等额多次支付复利计算。
3、它的的特点是:把上期末的本利和作为下一期的 本金,在计算时每一期本金的数额是不同的。主要应用于计算多次等额投资的本利终值和计算多次等额回款值。
复利的计算公式为
复利计算公式:F=P*(F/P.i.n)。
F是终值,P是现值,i是利率,n是计息的期数。复利计算的特点是:把上期末的本利和作为下一期的本金,在计算时每一期本金的数额是不同的。复利的本息计算公式是:F=P(1+i)^n。复利计算有间断复利和连续复利之分。按期(如按年、半年、季、月或日等)计算复利的方法为间断复利;按瞬时计算复利的方法为连续复利。在实际应用中一般采用间断复利的计算方法。
例如:本金为50000元,利率或者投资回报率为3%,投资年限为30年,那么,30年后所获得的本金+利息收入,按复利计算公式来计算就是:50000×(1+3%)^30。由于,通胀率和利率密切关联,就像是一个硬币的正反两面,所以,复利终值的计算公式也可以用以计算某一特定资金在不同年份的实际价值。只需将公式中的利率换成通胀率即可。
单利和复利的计算公式
单利:计算公式:I=P×R×N;复利:计算公式:F=P(1+i)^n
I=P×R×N;解释:I表示利息,P表示本金,R表示利率,N表示时间。
复利:计算公式:F=P(1+i)^n;解释:F表示终值,P表示本金,i表示利率或折现率,N表示计息期数。
单利就是利不生利,即本金固定,到期后一次性结算利息,而本金所产生的利息不再计算利息。复利其实就是利滚利,把上期末的本利和作为下一期的本金,在计算时每一期本金的数额是不同的。
在现实经济生活中,有时需要根据终值来确定其现在的价值即现值。例如,在使用未到期的票据向银行申请贴现时,银行按一定利率从票据的到期值中扣除自借款日至票据到期日的应计利息,将馀额付给持票人,该票据则转归银行所有。贴现时使用的利率称贴现率,计算出来的利息称贴现息,扣除贴现息后的馀额称为现值。
复利终值计算公式
复利终值计算公式F=P×(1+i)*n,即F=P×(F/P,i,n)。
复利终值公式:F=P×(1+i)*n,即F=P×(F/P,i,n)。其中,(1+i)*n称为复利终值系数,用符号(F/P,i,n)表示。复利是计算利息的一种方法。按照这种方法,每经过一个计息期,要将所生利息加入本金再计利息,逐期滚算,俗称利滚利。