小数如何分类?

纯小数、带小数、无限小数、有限小数。

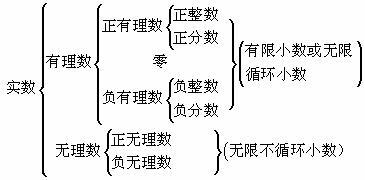
小数有两大类分类方法，一种是按照整数部分的情况分类，另一种是按照小数部分的情况分类。

1、按照整数部分的情况分类，可分为：

纯小数，是指整数部分为“0”的小数。例如0.3、0.226等，都是纯小数。

带小数，是指整数部分不为“0”的小数。例如1.638，223.745，等，都是带小数。

2、按照按照小数部分的情况分类，可分为：

有限小数，是指小数部分后有有限个数位的小数。如2.4768，0.524，6.3333333等，有限小数都属于有理数，可以化成分数形式。

无限小数，无限小数又可分为循环小数以及无限不循环小数。循环小数从小数部分的某一位起，一个数字或几个数字，依次不断地重复出现的小数叫做循环小数。如1/3=0.333333……等。循环小数亦属于有理数，可以化成分数形式。

无限不循环小数的小数部分则有无限多个数字，且没有依次不断地重复出现的一个数字或几个数字的小数叫做无限不循环小数，如圆周率π＝3.14159265358979323……等。无限不循环小数也就是无理数，不能化成分数形式。

小数分类

分为有限小数和无限小数。

1、有限小数：是小数点后面只有有限个不全为 “ 0”的数字的小数。 例如， 0.6， 0.49，6.064， 10.168，都是“有限小数” 。

2、无限小数：是小数点后面有无限多个不全为 “ 0” 的数字的小数。 例如， 0.333，3.1415926535897932384626，都是“无限小数” 。

在无限小数中，又有无限循环小数和无限不循环小数。

无限循环小数，一个无限小数，如果从小数部分的某一位起，都是由一个或几个数字依照一定的顺序连续不断地重复出现，这样的小数叫做“无限循环小数” ，简称“循环小数” 。

重复出现的一个或几个数字，叫做“循环节” 。记数时，在第一个循环节的第一个数字和最末一个数字上分别记上一个圆点（循环节只有一个数字的只记一个圆点） “·”，表示这个循环小数的这几个（或一个）数字重复出现。这样的圆点叫做“循环点” 。

在无限循环小数中，循环节从小数第一位（十分位）开始的，叫做“纯循环小数“。若小数点与第一个循环节之间还有不循环的数字，则这个循环小数便叫做“混循环小数“。

无限不循环小数，一个小数的数位无限多，而且小数位上的数字是不循环的，这种无限小数便叫做 “无限不循环小数” 。 周率（ π ）便是一个无限不循环小数 。

扩展资料：

小数与分数的转化：

有限小数化分数：化为十分之几（百分之几……）后约分。

纯循环小数化分数：循环节作为分子，循环节如果有一位，分母为9；循环节有两位，分母为99；循环节有三位，分母为999，依次类推。能约分的要约分。

混循环小数化分数：化为有限小数和纯循环小数之和后化简，无限不循环小数为无理数，不可以化为分数。

参考资料来源：百度百科-小数

小数的分类是什么？

小数有两大类分类方法，一种是按照整数部分的情况分类，另一种是按照小数部分的情况分类。

按照整数部分的情况分类，可分为：

1、纯小数，是指整数部分为“0”的小数。例如0.3、0.226等，都是纯小数。

2、带小数，是指整数部分不为“0”的小数。例如1.638，223.745，等，都是带小数。

有限小数

小数部分后有有限个数位的小数。如3.1465，0.364，8.3218798456等，有限小数都属于有理数，可以化成分数形式。

一个最简分数可以被化作十进制的有限小数当且仅当其分母只含有质因数2或5或两者。 类似的，一个最简分数可以被化作某正整数底数的有限小数当且仅当其分母之质因数为此基底质因数的子集。

如果按小数部分的什么来划分小数可以分为什么和什么小数

按小数部分的小数部分来划分，小数可以分为有限小数和无限小数。

一、有限小数

1、小数点后的小数个数有限，那么这个数叫做有限小数。

2、或者如果一个小数的小数点后数码，依次可以和实无穷的自然数数列 1，2，3，…，n，… 一一对应，那么这个小数就是无限小数。

3、如果一个小数的小数点后数码，从某个有限大的 n 之后全部为0，那么这个小数就是有限小数。从这种意义上讲，有限小数可以看作一种特殊的无限小数。

二、无限小数

1、无限小数是指经计算化为小数后，小数部分无穷尽，不能整除的数。包括分数和无理数。

2、从小数点后某一位开始不断地出重复现前一个或一节数码的十进制无限小数。如2.1666…，35.232323…等，被重复的一个或一节数码称为循环节。循环小数的缩写法是将第一个循环节以后的数码全部略去，而在保留的循环节首末两位上方各添一个小点。

小数分哪几种

第一种是按小数的小数部分的数位有限与无限分类。

小数可以分为有限小数和无限小数。而无限小数又可分为循环小数和无限不循环小数；循环小数可分为纯循环小数和混循环小数。

第二种分类方法是按小数的整数部分是否为零来分类。

小数可以分为纯小数和带小数。整数部分是零的小数叫做纯小数，纯小数一般比1小；整数部分不为零的小数叫做带小数，带小数一般都比1大。

扩展资料

切不可笼统地说小数可以分为纯小数、带小数，有限小数和无限小数。因为纯小数既可以是有限小数，又可以是无限小数，而无限小数既可以是纯小数，又可以是带小数，它们之间不是并列关系。

中国未引入西方的小数点前，中文有一套小数单位表示小数：分、釐、毫、丝、忽、微、纤等等，各单位是前一个的十分之一。如3.1416，读作“三又一分四釐一毫六丝”或“三个一分四釐一毫六丝”。

参考资料来源：百度百科-小数