一、实数的概念及分类？
实数，是有理数和无理数的总称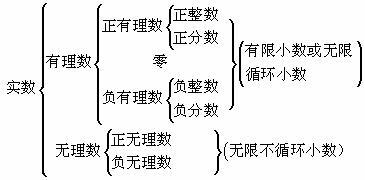
数学上，实数定义为与数轴上的实数，点相对应的数。实数可以直观地看作有限小数与无限小数，实数和数轴上的点一一对应。但仅仅以列举的方式不能描述实数的整体。实数和虚数共同构成复数。
实数可以分为有理数和无理数两类，或代数数和超越数两类。实数集通常用黑正体字母 R 表示。R表示n维实数空间。实数是不可数的。实数是实数理论的核心研究对象。
所有实数的集合则可称为实数系（real number system）或实数连续统。任何一个完备的阿基米德有序域均可称为实数系。在保序同构意义下它是惟一的，常用R表示。由于R是定义了算数运算的运算系统，故有实数系这个名称。
实数可以用来测量连续的量。理论上，任何实数都可以用无限小数的方式表示，小数点的右边是一个无穷的数列（可以是循环的，也可以是非循环的）。在实际运用中，实数经常被近似成一个有限小数（保留小数点后 n 位，n为正整数）。在计算机领域，由于计算机只能存储有限的小数位数，实数经常用浮点数来表示。
二、实数的分类
实数分为有理数和无理数。有理数分为整数和分数（分数即是小数），整数分为正整数，负整数，0。
三、实数的具体分类 实数的具体分类是哪些
1. 实数可以分为有理数和无理数。有理数可以分为整数和分数。整数分为正整数、0整数和负整数。分数分为正分数和负分数。
2. 实数可以分为正数、0和负数。正数可以分为正整数和正分数。负数可以分为负整数和负分数。
四、实数的分类是什么？
实数的分类：实数可以分为有理数和无理数两类。
有理数是整数可以看作分母为1的分数。正整数、0、负整数、正分数、负分数都可以写成分数的形式，这样的数称为有理数。有理数的小数部分是有限或循环小数。不是有理数的实数遂称为无理数。
无理数，也称为无限不循环小数，不能写作两整数之比。若将它写成小数形式，小数点之后的数字有无限多个，并且不会循环。常见的无理数有非完全平方数的平方根、π和e（其中后两者均为超越数）等。无理数的另一特征是无限的连分数表达式。
实数的性质：
1、封闭性
实数集对加、减、乘、除（除数不为零）四则运算具有封闭性，即任意两个实数的和、差、积、商（除数不为零）仍然是实数。
2、有序性
实数集是有序的，即任意两个实数a、b必定满足并且只满足下列三个关系之一：a＜b，a=b，a＞b。
3、传递性
实数大小具有传递性，即若a＞b，且b＞c，则有a＞c。
4、阿基米德性质
实数具有阿基米德性质，即（倒A）a，b∈R，若a＞0，则∃正整数n，na＞b。
5、稠密性
R实数集具有稠密性，即两个不相等的实数之间必有另一个实数，既有有理数，也有无理数。
6、完备性
作为度量空间或一致空间，实数集合是个完备空间，
