一、邻补角的定义是什么 关于什么是邻补角的介绍
1、两个角有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角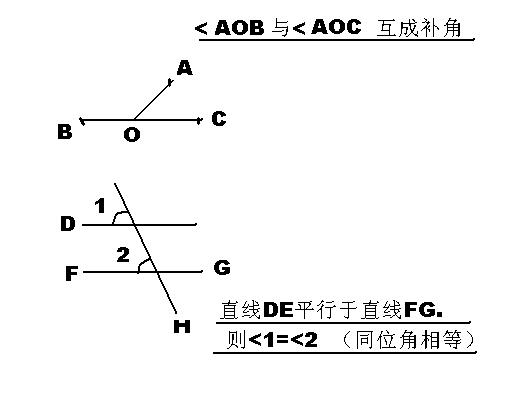
概述图中，∠AOC有两个邻补角：∠AOD和∠COB。（注：补角只注重数量关系两角之和是180°，即无论是否有公共边均可，但邻补角还要注重位置上的关系)。
2、邻补角（Adjacent Supplementary Angle或adjacent angles on a straight line ），两个角有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，叫做邻补角。（也就是邻补角的定义）
二、邻补角的定义是什么
两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角，叫做邻补角。接下来分享邻补角的定义。
邻补角的定义
两个角有一条公共边，它们的另一条边互为反向延长线。具有这种关系的两个角，互为邻补角。图中，∠AOC有两个邻补角：∠AOD和∠COB。（注：补角只注重数量关系两角之和是180°，即无论是否有公共边均可，但邻补角还要注重位置上的关系。）
邻补角的性质
一个角与它的邻补角的和等于180°。
如果两个角互为邻补角，那么它们的角平分线互相垂直。
补角的定义及性质
补角的定义：若两角之和满足180°+2kπ（k∈Z），那么这两个角互为补角。其中一个角叫做另一个角的补角。
备注：两个角的所在位置并不影响其互为补角，要判断两个角是否互补，只需满足：两个角的和等于180°+360°k,k∈Z。
补角的性质：同角或等角的补角相等。
它包括以下两方面的内容：
1.同角的补角相等。即：若∠A+∠B=180°,∠A+∠C=180°，则∠C=∠B
2.等角的补角相等。即：∠A+∠B=180°，∠D+∠C=180°，∠A=∠D，则∠C=∠B
三、什么叫邻补角定义
两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角，叫做邻补角。(也就是邻补角的定义)
四、邻补角的定义
邻补角（Adjacent Supplementary Angle或adjacent angles on a straight line），两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角，叫做邻补角。（注：补角只注重数量关系两角之和是180°，即无论是否有公共边均可，但邻补角还要注重位置上的关系)。
扩展资料：
一、特征识别
1、具有一个公共的顶点。
2、有一条公共边。
3、两个角的另一边互为反向延长线。
4、邻补角是成对出现的，而且是互为邻补角。
5、互为邻补角的两角相拼为平角。
6、互为邻补角的两角互补，即相加为180度。
二、辨析原则
邻补角包括两个方面的要求：两角的位置关系、数量关系。
补角：指的是数量关系满足两角之和等于180度；
邻角：指的是位置关系满足两角有公共的顶点和公共的边。
参考资料来源：百度百科－邻补角
五、邻补角的定义和性质
邻补角的定义是两个角有一条公共边，它们的另一条边互为反向延长线，具有这种关系的两个角，互为邻补角。图中，∠AOC有两个邻补角:∠AOD和∠COB。(注:补角只注重数量关系两角之和是180°，即无论是否有公共边均可，但邻补角还要注重位置上的关系)。
邻补角的性质是：一个角与它的邻补角的和等于180°；如果两个角互为邻补角，那么它们的角平分线互相垂直。
我们可以通过以下几点来识别邻补角：
1、具有一个公共的顶点。
2、有一条公共边。
3、两个角的另一边互为反向延长线。
4、邻补角是成对出现的，而且是互为邻补角。
5、互为邻补角的两角相拼为平角。
6、互为邻补角的两角互补，即相加为180度。
