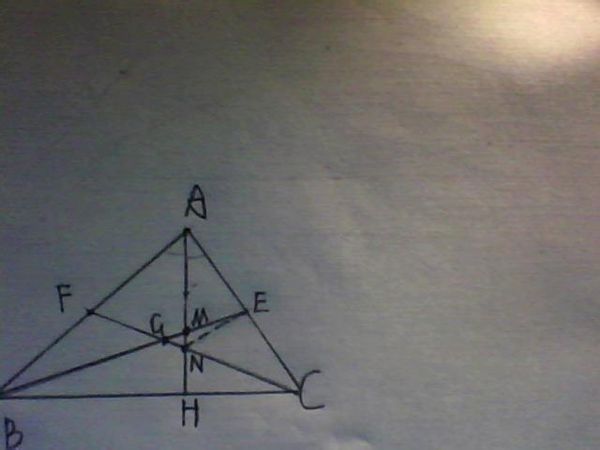
一、三角形四心是什么，有什么特点判定
外心:三边中垂线交点内心:三条角平分线交点重心:三边中线交点垂心:三边上的高的交点另外还有被称为"旁心"的点,是三角形一个角的平分线和另外2个角的外角平分线的交点,每个三角形有3个旁心
二、三角形的“四心”指哪四心？
三角形的四心是指三角形的重心、外心、内心、垂心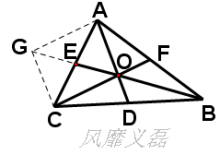
当且仅当三角形是正三角形的时候，重心、垂心、内心、外心四心合一心，称做正三角形的中心。
1、数学上的重心是指三角形的三条中线的交点，其证明定理有燕尾定理或塞瓦定理，应用定理有梅涅劳斯定理、塞瓦定理。
2、三角形的三条高线的交点叫做三角形的垂心。锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外.
3、三角形三条内角平分线的交点叫三角形的内心。即内切圆的圆心。内心是三角形角平分线交点的原理：经圆外一点作圆的两条切线，这一点与圆心的连线平分两条切线的夹角。
4、外心是一个数学名词。是指三角形三条边的垂直平分线也称中垂线的相交点。用这个点做圆心可以画三角形的外接圆。
扩展资料
一、垂直性质
三角形的三条垂直平分线必交于一点
已知：△ABC中，AB,AC的垂直平分线DO,EO相交于点O
求证：O点在BC的垂直平分线上
证明：连结AO,BO,CO，∵DO垂直平分AB，∴AO=BO
∵EO垂直平分AC，∴AO=CO
∴BO=CO
即O点在BC的垂直平分线上
二、外心性质
1、三角形三条边的垂直平分线交于一点，该点即为三角形外接圆的圆心.
2、三角形的外接圆有且只有一个，即对于给定的三角形，其外心是唯一的，但一个圆的内接三角形却有无数个，这些三角形的外心重合。
3、锐角三角形的外心在三角形内；钝角三角形的外心在三角形外；直角三角形的外心与斜边的中点重合
4、OA=OB=OC=R
5、∠BOC=2∠BAC，∠AOB=2∠ACB，∠COA=2∠CBA
6、S△ABC=abc/4R
参考资料来源：百度百科-三角形的四心
