一、切线方程和法线方程的关系
切线方程和法线方程的关系是相互垂直，公共点是切点，过切点与切线垂直的直线为法线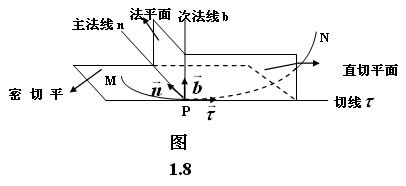
记曲线为y=f(x)则在点(a，f(a))处的切线方程为：y=f'(a)(x-a)+f(a)，法线方程公式：α*β=-1。
由基本函数的和、差、积、商或相互复合构成的函数的导函数则可以通过函数的求导法则来推导。
基本的求导法则：
1、求导的线性：对函数的线性组合求导，等于先对其中每个部分求导后再取线性组合。
2、两个函数的乘积的导函数：一导乘二+一乘二导。
3、两个函数的商的导函数也是一个分式：（子导乘母-子乘母导）除以母平方。
4、如果有复合函数，则用链式法则求导。
二、法线和切线的关系
切线与法线的关系：（1）相互垂直；（2）公共点是切点，过切点与切线垂直的直线为法线。
切线斜率与法线斜率关系
由于切线与法线垂直
所以切线的斜率乘以法线的斜率=-1
怎么求函数的切线方程和法线方程
(1)求出y=f(x)在点x0处的纵坐标y0=f(x0)
(2)求导：y′=f′(x)
(3)求出在点x=x0处切线的斜率k=f′(x0)，在点x=x0处法线斜率=-1/k=-1/f′(x0)
(4)根据点斜式，写出切线方程：y=k(x-x0)+y0=f′(x0)*{x-x0}+f(x0)
写出切线方程：y=(-1/k)(x-x0)+y0={-1/f′(x0)}*{x-x0}+f(x0)
如果有要求，可根据要求进一步化成一般式或斜截式。
三、切线与法线的关系
切线与法线的关系相互垂直。
切线与法线的关系:(1)互相垂直；(2)公共点是切点。在几何学上，切线指的是一条刚好接触曲线上一点的直线。
如果切点垂直于切线，法线和切线之间的关系就是法线。
切线与法线的关系:(1)互相垂直；(2)公共点是切点。
切线几何上，切线指的是一条直线，它只接触曲线上的一点。更准确地说，当切线穿过曲线上的某一点(即切点)时，切线的方向与曲线上该点的方向相同。在平面几何中，与圆只有一个公共交点的直线称为圆的切线。
法线定义法线，总是垂直于平面的虚线。曲线的法线是垂直于曲线上一点的切线的直线，而曲面上一点的法线是指穿过该点并垂直于该点的切面的直线(即矢量)。
在物理学中，在入射点垂直于镜子的直线叫做法线。
四、法线和切线的关系是什么
法线和切线的关系是相互垂直，公共点是切点。几何上，切线指的是一条刚好触碰到曲线上某一点的直线。法线是始终垂直于某平面的虚线。在物理学中过入射点垂直于镜面的直线叫做法线。 扩展资料 法线和切线的关系是相互垂直，公共点是切点。几何上，切线指的`是一条刚好触碰到曲线上某一点的直线。法线是始终垂直于某平面的虚线。在物理学中过入射点垂直于镜面的直线叫做法线。
五、法线与切线的关系
切线有一个方程式，垂直与其的一个向量即为其法向量。与法线平行。
是指与切线垂直的向量，与法线是一样的只是说法不一样。
六、切线与法线区别?
过切点与切线垂直的直线为法线.
切线与法线的关系：（1）相互垂直；（2）公共点是切点.
