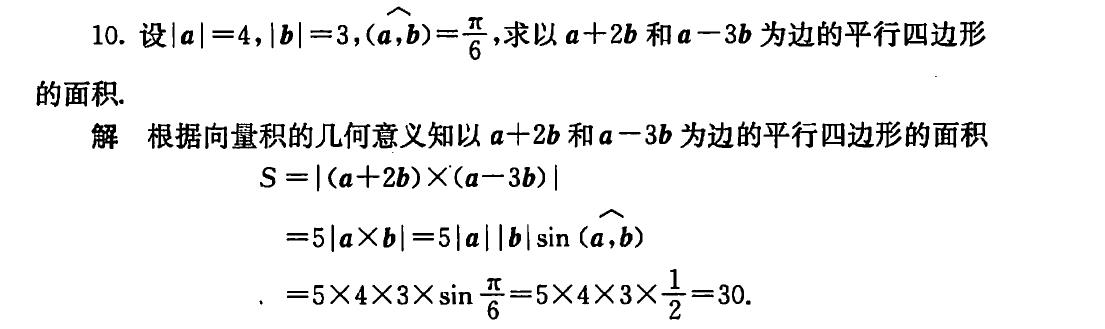一、二维向量叉乘公式(向量叉乘公式行列式)
1、三维向量叉乘公式
2、二维向量叉乘公式。
3、两个向量叉乘公式。
4、空间向量叉乘公式。
1.向量叉乘公式:|向量c|=|向量a×向量b|=|a||b|sin。
2.在数学中,向量(也称为欧几里得向量、几何向量、矢量),指具有大小(magnitude)和方向的量。
3.它可以形象化地表示为带箭头的线段。
4.箭头所指:代表向量的方向。
5.线段长度:代表向量的大小。
6.和向量对应的量叫做数量(物理学中称标量),数量(或标量)只有大小,没有方向。
7.向量的记法:印刷体记作黑体(粗体)的字母(如a、b、u、v),书写时在字母顶上加一小箭头“→”。
8.如果给定向量的起点(A)和终点(B),可将向量记作AB(并于顶上加→)。
9.在空间直角坐标系中,也能把向量以数对形式表示,例如xOy平面中(2,3)是一向量。
二、向量叉乘公式是什么啊
叉乘,也叫向量的外积、向量积。顾名思义,求下来的结果是一个向量,记这个向量为c。
|向量c|=|向量a×向量b|=|a||b|sin
向量c的方向与a,b所在的平面垂直,且方向要用“右手法则”判断(用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向)。
因此
向量的外积不遵守乘法交换率,因为向量a×向量b= -
向量b×向量a
在物理学中,已知力与力臂求力矩,就是向量的外积,即叉乘。
将向量用坐标表示(三维向量),
若向量a=(a1,b1,c1),向量b=(a2,b2,c2),
则
向量a×向量b=
| i j k |
|a1 b1 c1|
|a2 b2 c2|
=(b1c2-b2c1,c1a2-a1c2,a1b2-a2b1)
(i、j、k分别为空间中相互垂直的三条坐标轴的单位向量)。
数学中,既有大小又有方向且遵循平行四边形法则的量叫做向量(vector)。
向量
向量
有方向与大小,分为自由向量与固定向量。
数学中,把只有大小但没有方向的量叫做数量,物理中称为标量。例如距离、质量、密度、温度等。
注:在线性代数中(实数空间/复数空间)的向量是指n个实数/复数组成的有序数组,称为n维向量。α=(a1,a2,…,an) 称为n维向量。其中ai称为向量α的第i个分量。
("a1"的"1"为a的下标,"ai"的"i"为a的下标,其他类推)
在编程语言中,也存在向量。向量有起点,有方向。常用一个带箭头的线段表示。
三、二维向量叉乘公式是什么?
二维向量叉乘公式a(x1,y1),b(x2,y2),则a×b=(x1y2-x2y1),不需要证明的就是定义的运算。
三维叉乘是行列式运算,也是叉积的定义,你把第三维看做0代入就行了。
扩展资料
性质:
1、行列式与它的转置行列式相等。
2、互换行列式的两行(列),行列式变号。
3、如果行列式有两行(列)完全相同,则此行列式为零。
4、行列式的某一行(列)中所有的元素都乘以同一数k,等于用数k乘此行列式。
5、行列式中某一行(列)的所有元素的公因子可以提到行列式符号的外面。
6、行列式中如果有两行(列)元素成比例,则此行列式等于零。
7、把行列式的某一列(行)的各元素乘以同一数然后加到另一列(行)对应的元素上去,行列式不变。
参考资料:百度百科 -向量积
四、二维向量叉乘公式
二维向量也可以进行叉积运算,对于向量(x1,y1)、(x2,y2)(跟lz给的不太一样……)叉积运算结果为x1*y2-x2*y1,可以把二维向量叉积运算所得的结果看做一个数字,虽然更准确地说它应该是一个伪向量,方向垂直于(x1,x2)、(x2,y2)所在平面,相应的遵循左手或右手定则.不知道能不能帮到lz……