一、什么是折射角和入射角
入射角（incident angle）是入射光线与入射表面法线的夹角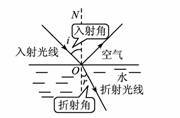
在光学里，入射角是原因，反射角是结果，反射角等于入射角。
入射角是指射到镜面上的光线与法线所形成的夹角，反射角是指被镜面反射的光线与法线形成的夹角，法线是过入射点垂直于镜面的直线。光线被镜面反射的传播路线可以用下图表示，其中，ADP为入射角 [1] ，
折射光线与法线的夹角叫折射角。其折射情况遵循折射定律。光从空气斜射入水或其他介质中时，折射角小于入射角，当入射角增加时，折射角随着增加。光从水中或其他介质斜射入空气中时，折射角大于入射角。当光从空气垂直射入（或其他介质射入），传播方向不改变。
二、什么是入射角折射角
入射角是入射光线与法线的夹角，折射角是折射光线与法线的夹角。
光从空气斜射入水或其他介质中时，折射角小于入射角，当入射角增加时，折射角随着增加。
光从水中或其他介质斜射入空气中时，折射角大于入射角。当光从空气垂直射入（或其他介质射入），传播方向不改变。
扩展资料：
光从空气斜射入水或其他介质中时，折射角小于入射角，当入射角增加时，折射角随着增加。光从水中或其他介质斜射入空气中时，折射角大于入射角．当光从空气垂直射入（或其他介质射入），传播方向不改变。
入射光线垂直界面入射时，折射角等于入射角等于0°；光从空气斜射入水等介质中时，折射角小于入射角；光从水等介质斜射入空气中时，折射角大于入射角。
三、什么是光的折射角（最好画图说明）
我们说光线是沿直线传播的，那是指光在同一种介质中传播的情况，如果光从一种介质进入到另一种介质，比如光线从空气进入到水中时，就会发生折射（当然，反射肯定还是存在的）
折射角是指从空气斜射入水（或其他介质）中的光线向法线偏折时，折射的光线和法线的夹角
ps：
如果是光从水（或其他介质）中斜射入空气的话，折射光线会偏向与法线相反的位置，但折射的光线和法线的夹角还是折射角
若光线垂直射入的话，那么折射角为0°（同入射角、反射角一样都是0°）
--------------------------------------------------------有什么问题就再说吧，我明天还要交两篇作文TAT，很抱歉我不会用电脑画图；可能我还有一些知识点没说，你看看其他的吧
四、什么是折射角和入射角？
折射角和入射角都是针对光来说的，都是光与法线的夹角。如入射光线与法线的夹角叫入射角，折射光线与发现的夹角叫折射角。
五、什么叫折射角
折射图
折射光线与法线的夹角叫折射角。其折射情况遵循折射定律。
光的折射定律：三线同面，法线居中，空气中角大，光路可逆．
﹙1﹚折射光线，入射光线和法线在同一平面内．
﹙2﹚折射光线和入射光线分居在法线两侧．
﹙3﹚光从空气斜射入水或其他介质中时，折射角小于入射角，当入射角增加时，折射角随着增加．光从水中或其他介质斜射入空气中时，折射角大于入射角．当光从空气垂直射入（或其他介质射入），传播方向不改变。
3．应用：从空气看水中的物体，或从水中看空气中的物体看到的是物体的虚像，看到的位置比实际位置高。
折射规律分三点：（1）三线一面
（2）两线分居（3）两角关系分三种情况：①入射光线垂直界面入射时，折射角等于入射角等于0°；②光从空气斜射入水等介质中时，折射角小于入射角；③光从水等介质斜射入空气中时，折射角大于入射角(但存在于空气中的角总是一个大角）
编辑本段费马原理
础功壁嘉撰黄辩萎菠联
费马原理：光在传播过程中遵循“光程最短”的原则（也就是传播最快）。据此，可以用数学的方法可以证明折射的规则：
Sini:Sinγ=v1:v2
i是入射角，γ是反射角，v1,v2是两种介质中的光速。
又因真空中的光速c最大且恒定，故规定
n=c/v
n就是折射率。
显然，有
n2:n1=v1:v2=Sini:Sinγ
证明过程：下面我就来说说光为什么这样传播：
一束光线由空气中A点经过水面折射后到达水中B点，已知光在空气和水中传播的速度分别是v1和v2，光线在介质中总是沿着耗时最少的路径传播。试确定光线传播的路径。
设A点到达水面的垂直距离为AO=h1，B点到水面的垂直距离为BQ=h2，x轴沿水面过点O、Q，其中OQ的长度为l
由于光线总是沿着耗时最少的路径传播，因此光线在同一介质内必沿着直线传播。设光线的传播路径与x轴的交点为P，
OP=x，则光线从A到B的传播路径必为折线APB，其所需要的传播时间为：
T（x）=sqrt（h1^2+x^2）/v1
+
sqrt[h2^2+(l-x)^2]
/v2
，
x∈[0,l].
下面来确定x满足什么条件时，T（x）在[0，l]上取得最小值。
由于
T‘（x）=1/v1
*
x/sqrt(h1^2+x^2)
-
1/v2
*
(l-x)/sqrt（h2^2+(l-x)^2），
x∈[0,l]
注释：T'（x）为T（x）的一阶导数
T''（x）=1/v1
*
h1^2/sqrt[(h1^2+x^2)^3]
+
1/v2
*
h2^2/sqrt[(h2^2+(l-x)^2)^3]
>
，
x∈[0,l]
T''（x）为T（x）的二阶导数
T'（0）<0，T'(l)>0，
又T'(x)在[0,l]上连续，故T'(x)在（0,l）内存在唯一零点x0是T（x）在（0,l）内的唯一极小值点，从而也是T（x）在[0,l]上的最小值点。
设x0满足T'（x）=0，即
x0
/
v1*sqrt(h1^2+x0^2)
=
(l-x)
/
v2*sqrt(h2^2+(l-x0)^2)
记
x0
/
sqrt(h1^2+x0^2)
=sinθ1
，
(l-x0)
/sqrt[h2^2+(l-x0)^2]
=sinθ2
就得到
sinθ1/v1
=sinθ2/v2
这就是说，当P点满足以上条件时，APB就是光线的传播路径。上式就是光学中著名的折射定律，其中θ1，θ2分别是光线的入射角和折射角。
一般来说：空气中的折射角>玻璃中的折射角>水中的折射角
开放分类：
参考资料：baike.baidu.com/view/522739.htm
