一、|x|,x=0是跳跃间断点吗
一楼自己也没有搞清楚,就批评起来,并不可取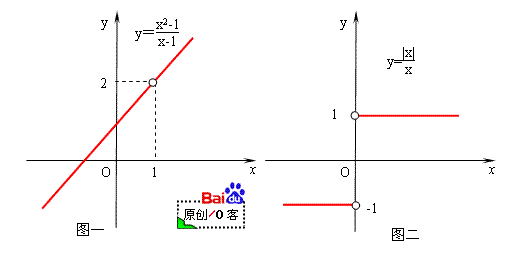
两个图形非常类似,下面比较一下两个图形的异同(Similarity and Difference):
1、两者都是反正切函数,图形大同小异:
两者的值域稍有差异:
arctan x 的值域是:(-π/2,π/2)
arctan 1/x 的值域是:(-π/2,0)∪(0,+π/2)
两者的定义域也稍有差异:
arctan x 的定义域是:(-∞,+∞)
arctan 1/x 的定义域是:(-∞,0)∪(0,+∞)
2、arctan x 是增函数,无间断点:
在第三象限从 -π/2 一路上升至原点(上凹),在第一象限从原点一路上升至 π/2 (下凹);
arctan 1/x 是减函数,x=0 是跳跃型间断点:
在第二象限从 π/2 一路下降至原点(下凹),在第四象限从原点一路下降至 -π/2 (上凹)。
当 x → 0-, arctan 1/x → -π/2;
当 x → 0+, arctan 1/x → +π/2.
∴ x = 0 是跳跃型间断点(左极限≠右极限,就是跳跃)
因为是跳跃型间断点,不是可去型间断点。补充定义,意义不大。
要根据具体实际问题,补充定义。f(0) can be any number.
3、arctan x 和 arctan 1/x 有共同的渐近线(Asymptote) ±½π
4、在任何一点,他们的斜率(|dy/dx|)的绝对值是相等的,曲率半径也是相等的。
整体上,图形是对称的。
二、第一类间断点,第二类间断点,可去间断点,跳跃间断点的概念分别是什么?
可去间断点和跳跃间断点称为第一类间断点,其它间断点称为第二类间断点。
可去间断点:函数在该点左极限、右极限存在且相等,但不等于该点函数值或函数在该点无定义。如函数y=(x^2-1)/(x-1)在点x=1处。
跳跃间断点:函数在该点左极限、右极限存在,但不相等。如函数y=|x|/x在点x=0处。
无穷间断点:函数在该点可以无定义,且左极限、右极限至少有一个为∞,如函数y=tanx在点x=π/2处。
连续与非连续的定义
设函数y=f(x)在点x0 的某一去心邻域内有定义,如果函数f(x)当x→x0 时的极限存在,且等于它在点x0 处的函数值f(x0),即limf(x)=f(x0)(x→x0),那么就称函数f(x)在点x0 处连续。
不连续情形:
1、在点x=x0没有定义;
2、虽在x=x0有定义但lim(x→x0)f(x)不存在;
3、虽在x=x0有定义且limf(x)(x→x0)存在,但lim f(x)≠f(x0)(x→x0)时则称函数在x0处不连续或间断。
三、如图的跳跃间断点是什么?
跳跃间断点:首先间断点是指函数在该点不连续,显然x=0会导致1/x的分母
四、x=o是为什么是跳跃间断点?高数~
因为如果从数轴正方向趋于0时,分子分母同趋于无穷大,用洛必达法则,分子分母同时对x求导,于是极限为1,但是,如果从负方向趋于0时,分子趋于-1,而分母趋于1,极限为-1,当x从负轴往正轴变化时,在0点就发生跳跃
五、什么是跳跃间断点
跳跃间断点是使指左极限f(x-)与右极限f(x+)都存在的间断点,且f(x-)≠(x+),可去间断点和跳跃间断点属于第一类间断点,左右极限存在是前提。
间断点分为可去间断点、跳跃间断点、无穷间断点、震荡间断点,左右极限相等,但不等于该点函数值f(x0)或者该点无定义时,称为可去间断点。非第一类间断点即为第二类间断点。